优化 | 二部图最大匹配问题的精确算法详解(HK算法和匈牙利算法):一份让您满意的【理论介绍+代码实现】学习笔记
上一个版本写的比较简略,这个版本做了很多补充解释和完善。
上个版本的文章链接:
二部图最大匹配——HK算法作者:张瑞三,四川大学,硕士在读 邮箱:zrssum3@stu.scu.edu.cn
审校:刘兴禄,清华大学,清华-伯克利深圳学院 邮箱:hsinglul@163.com
二分图最大匹配问题是一个经典问题,顾名思义就是寻找二分图两个独立集合中的最大匹配(最大匹配中匹配指的是一对一匹配),例如相亲活动中,男生集合和女生集合,相互有意的即存在配对的可能(不排除花心大萝卜的存在,同时对多个异性有好感),相亲成功的最多的配对情况就是我们要找的最大匹配。在很多领域有重要应用,例如求最小点覆盖或者最大独立集,但是它却可以在多项式时间内精确求解,因此该问题不是NP hard。
目前已经有多种在多项式时间内精确求解二部图最大匹配问题的算法,如Kuhn-Munkres algorithm(匈牙利算法)和Hopcroft–Karp algorithm(以下简称HK算法)等。今天我们介绍的主角就是HK算法,它是一种非常高效的求解二部图最大匹配的一种精确算法(复杂度为 ,这里的
是图中点数,
是边数)后面我们会进行证明),也就是说——该算法可以得到最优解。HK算法通过不断寻找图中的增广路,从而找到可以提升当前解的方向,进而通过算法迭代,不断改进当前解,直到找不到任何增广路为止,此时,说明当前解已经达到最优。在最后我们也提供了HK算法中寻找增广路径的python代码供以参考。
- 霍普克洛夫特-卡普算法(Hopcroft–Karp algorithm) 该算法由John Hopcroft和Richard Karp(1973)发现。正如之前的匹配方法,如匈牙利算法和Edmonds(1965)的工作一样,Hopcroft-Karp算法通过寻找增广路径反复增加部分匹配的大小:在进入和离开之间交替的边缘序列。
在学习HK算法之前,需要补充一些知识点,以便更好地理解算法结构。
首先我们解决的是二分图的最大匹配问题,所以我们需要先对二分图进行了解;其次我们去找最大匹配的时候是通过迭代寻找增广路径,所以增广路径的定义需要明确。
看到目录的同学可能会问,是讲HK算法的,为什么学前还要学习匈牙利算法(KM)呀?
回答:实际上HK算法是在KM算法上的优化,KM算法在每次迭代中,只是找到一条增广路,然后基于该增广路,对当前解进行改进。但是每次迭代中,却往往存在多条增广路,如果能找到多条增广路,算法效果会得到进一步提升。而HK算法正式利用了这一点,在每一次算法迭代中,同时使用了DFS和BFS,因此可以在单次迭代中找到多条增广路,从而进一步提升了效率,缩小了算法复杂度。
定义:二分图(又名二部图),是图论中的一种特殊模型。设 是一个无向图,如果顶点
可分割为两个互不相交的子集
,并且图中的每条边
所关联的两个顶点
和
分别属于这两个不同的顶点集
,则称图
为一个二分图。
简而言之,就是顶点集 可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
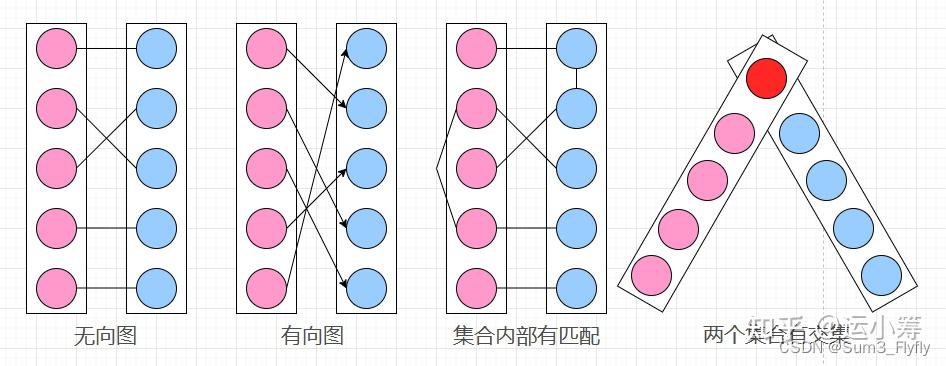
我们把上图中四个图编个号:①-④
②图很明显其中的边是有向的;
③图则是存在集合内部的边;
④图的两个集合存在了交集。
综上②、③、④都违反了二分图的定义,只有①图完美的符合二分图的定义,所以①图是一个二分图。
- 匹配:在图论中,一个“匹配”就是一个“边”的集合,其中任意两条边都没有公共顶点。
- 最大匹配:一个图的匹配集合中,所含匹配边数最多的匹配,或者说覆盖的点最多,称为这个图的最大匹配。
- 完美匹配:当一个图的匹配覆盖了所有的点,那么它就是一个完美匹配。

当然,可以看出完美匹配一定是最大匹配,所有的点都已经被覆盖,我们也找不到新的增广路径了。 如上图中的“一个匹配”中就仅是一个普通的匹配,而且我们很容易发现一条增广路径:2-B-5-C,然后就得到了最后的“最大匹配”的结果。
增广路径需要满足以下三个条件:
① 开始于一个未配对的向量
② 终止于一个未配对的向量
③ 路径中的节点在匹配和不匹配之间交替
在上面讲解最大匹配的配图中,我们就通过增广路径找到了最大匹配,我们来将这个过程分解一下:
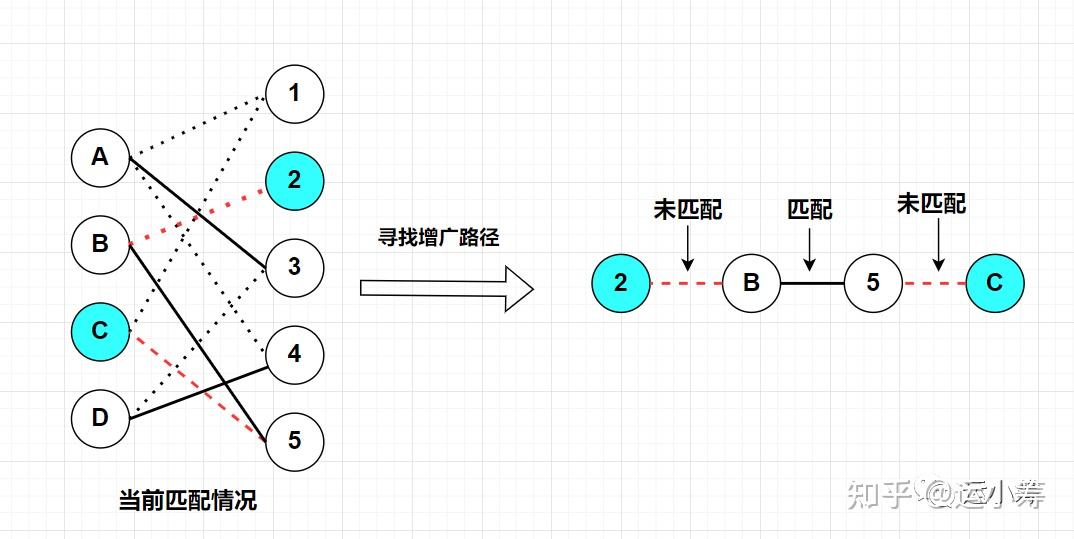
然后我们将配对的边断开,再把未配对的边连上:
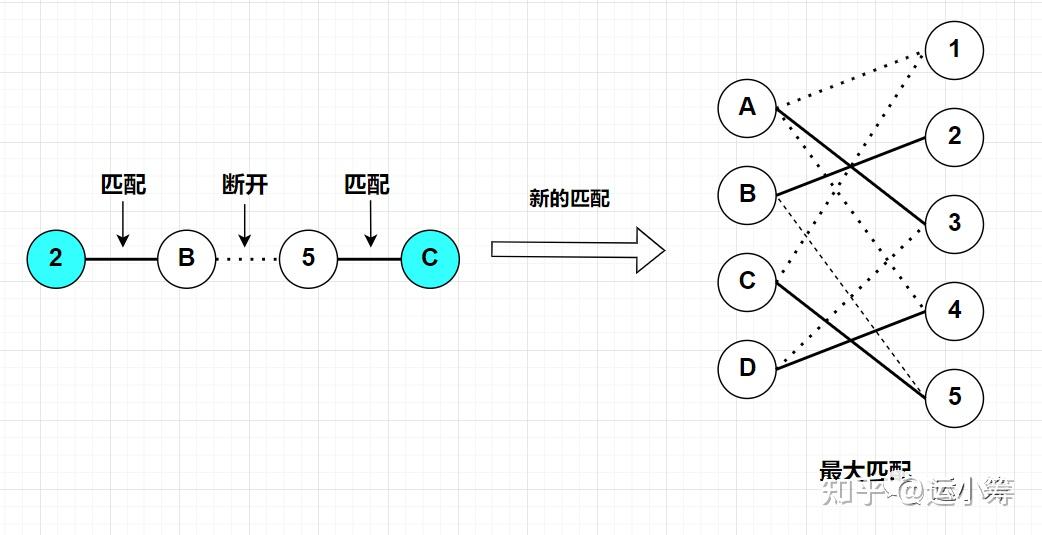
可以看到,经过这一次操作,图中的匹配由原来的3对匹配,变成了4对匹配。
不难发现,当我们找到一条增广路径的时候,未匹配边的数量比已匹配边的数量恰好多1。所以如果将一条增广路径中匹配的边断开,并将所有的未匹配边变成匹配边,就得到了一个更优的解(匹配+1)。
如果图中找不到任何增广路,说明该解不能被再次改进,当前解就是最优解了。这也是为什么找不找得到增广路是判断是否达到最优的充要条件。
上面提到了HK算法通过BFS寻找多条增广路径的,所以在这里需要先介绍一下BFS。
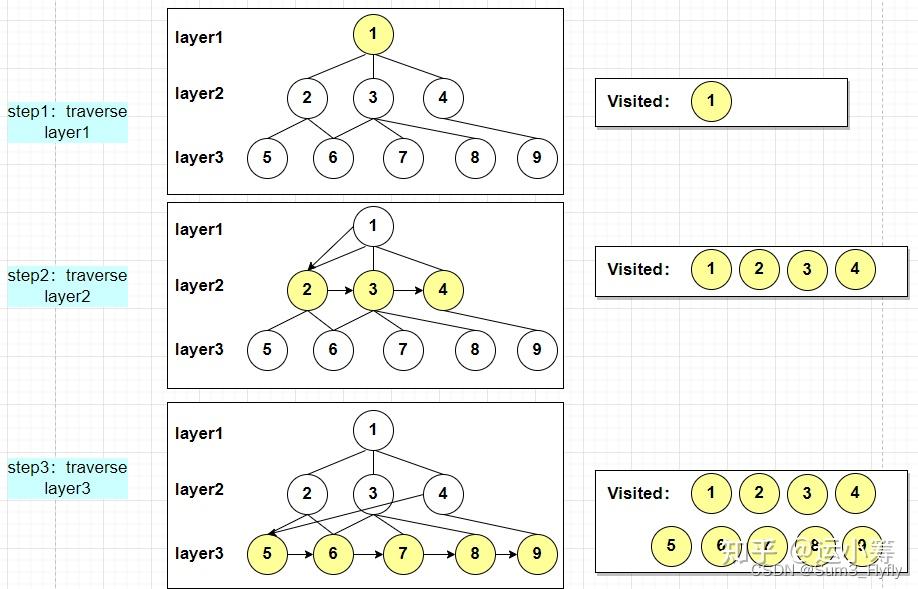
广度优先搜索(也称宽度优先搜索,缩写BFS)是连通图的一种遍历算法这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。基本过程,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止。
已知图 ,设
是其中的一个源顶点,按和
由近到远的遍历所有能到达的点,即存在边
连接两个点,并计算
到所有这些顶点的距离(最少边数),该算法同时能生成一棵根为
且包括所有可达顶点的宽度优先树。这样每一层全部都遍历完再遍历下一层的思想就是“广度优先”。
- step1:将图中所有结点储存在队列中,代码是使用python实现的,可以使用有序的数据结构来实现,按照所属层数来创建相应index的列表(HK算法交替路的始末)
- step2:从最上层中取出第一个端点
,从该起始点出发,访其未访问的所有匹配点
,并将已经访问的点从队列中删除;
- step3:对所有点重复step2:,直至队列为空。
KM算法和HK算法都是通过DFS来寻找增广路径的,所以也需要介绍一下DFS。
深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
已知图 ,设
是其中的一个源顶点,从最近的可到达的点中选择一个,然后按照这样的步骤,一直找到一个根节点,这便是一条路径,这样找到所有的路径。这种“一条路走到底”的思想便是”深度优先“。
- step1:从选择的源顶点
出发,选择一个邻接点
,再选择
的邻接点,直到访问到根节点;
- step2:从这条路径的根节点返回上一层,寻找是否存在同层的点,有则遍历同层点的路径,按照层数逐渐向上层寻找,按照上述步骤遍历所有的路径;
- step3:对所有匹配邻接点,按照step1和step2遍历所有路径;
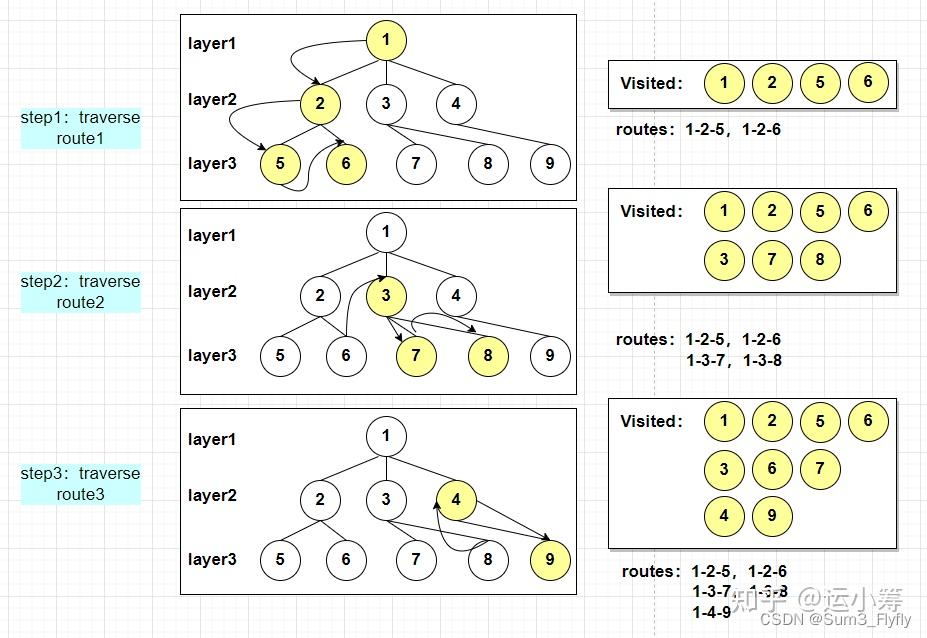
这里的遍历顺序就是:1-2-5-6-3-7-8-4-9
以下我们假设有一个二部图 ,其中
中包含两个端点集合
和
,
是两个端点集合的配对关系的边。
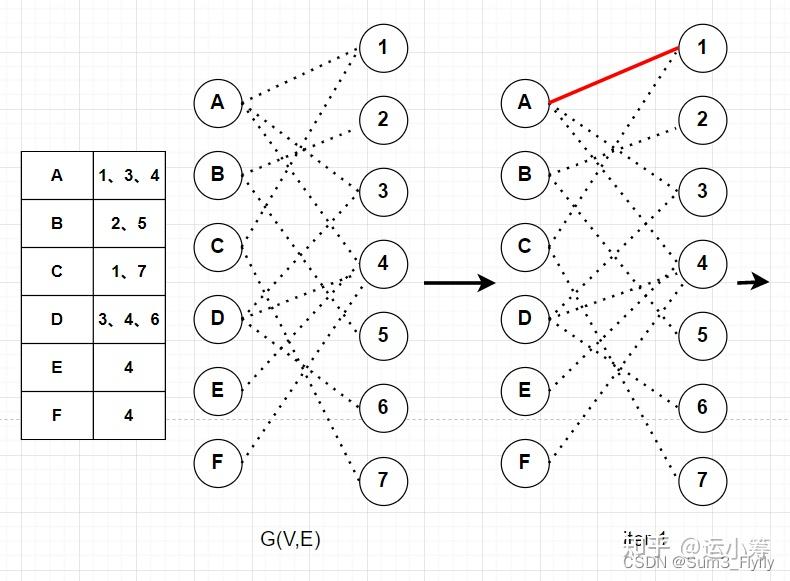
匈牙利算法的计算过程:匈牙利算法是用DFS来寻找增广路的。它从每个未匹配的的点开始,如果直接就找到了
中未匹配的点那么直接返回;若找到
已匹配的点,那么从该点匹配的点出发继续DFS。
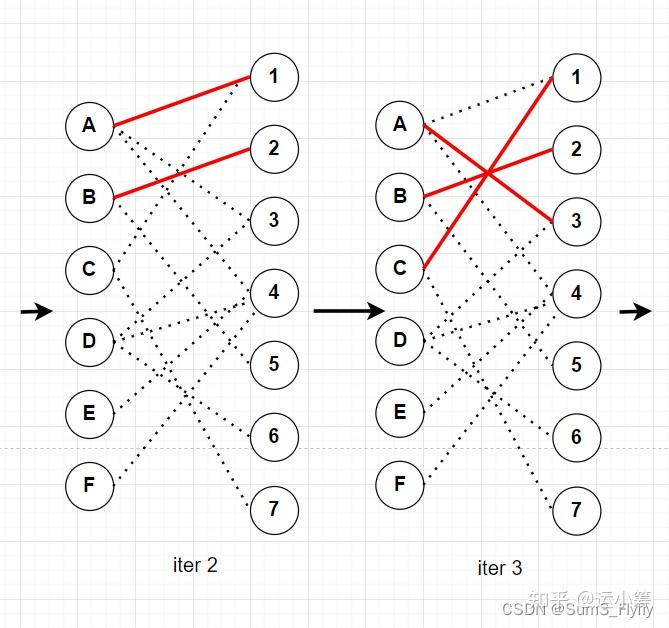
这是我们说明一下,在第三次迭代的时候,C点的第一个匹配点1已经与A匹配了,于是从c出发找一条交替路径:C-1-A-4,这条交替路也是一个增广路。
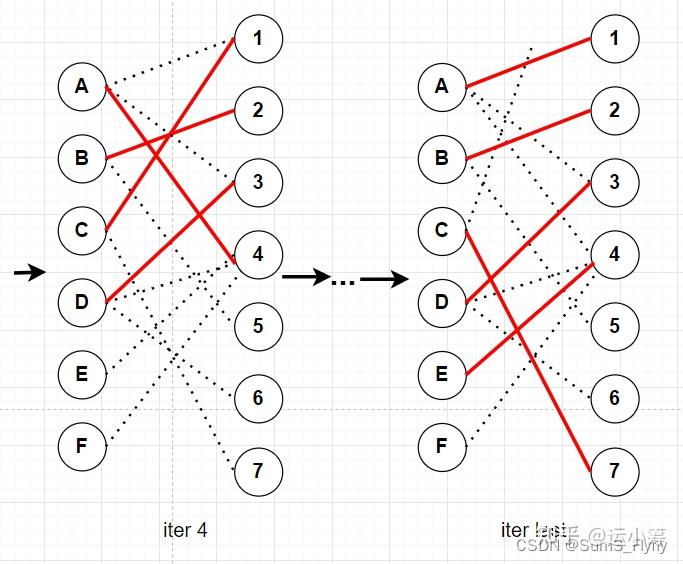
不难发现,KM算法每次迭代都是多遍历一个点,以及对应的边,所以匈牙利算法的复杂度为 。(应用到不同的问题上可能会有不同,复杂度跟数据结构也有关)
- 交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。
- 增广路(agumenting path):从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路。即
,且
。
- 最小点覆盖(Konig定理):假如选了一个点就相当于覆盖了以它为端点的所有边,你需要选择最少的点来覆盖所有的边。
- 最小割定理是一个二分图中很重要的定理:一个二分图中的最大匹配数等于这个图中的最小点覆盖数。
证明:设图,设最大匹配为
,那么根据最小点覆盖我们覆盖所有匹配的边则至少需要
个点,即选中的点全是最大匹配中的点,所以

其次,设我们从选择最小点集覆盖,则最小点集覆盖中的每个点都能找到至少一条只有一个点在匹配集中的边,如果没有就说明与该点存在匹配关系的的点
都被另外的一个
的点覆盖,那么就说明该点没有必要被覆盖,就与最小点集覆盖定义矛盾,所以

于是我们得出结论
Hopcroft-Karp 算法在每一次迭代中,都是基于当前的解(即当前的匹配)去寻找增广路径,如果有增广路径存在,说明当前解还不是最优解,可以理解为我们在精确性算法中的 ,还可以继续改进,提升解的质量;如果一次迭代结束后,找不到任何的增广路径,那么恭喜你找到了
的最优解——最大匹配。
为了方便解释伪代码,把问题定义一下: 设二部图,其中
中包含两个端点集合
和
,
是两个端点集合的配对关系的边,
是当前的匹配,
为最大匹配。
之前我们提到了HK算法在迭代中加入了BFS这一步,可以同时找多条增广路径,并且保证每次寻找到的增广路都是当前增广路中最短的从而优化效率。那么HK算法是如何通过BFS同时寻找多条增广路径的呢?也会有细心的小伙伴发现上面的图中有一个 ,恭喜你发现了它的秘密!
请回忆一下BFS的迭代过程,在迭代中BFS会将点进行分层,例如上面BFS示意图中,我们选择了根节点 ,那么
就在
中,那么与
有直接配对关系的点就会被放到
,然后再依次对
中的点进行这个操作,直到遍历所有需要遍历的点(只有在第一次才会遍历所有的点)。
在BFS结束后,我们就得到了一个有层次之分的”树“,从树的顶端到根部就构成了一个交替路,再通过DFS遍历这个交替路去寻找增广路径,但是每层都可能存在很多的点,而且相邻的层次中的点又具有配对关系,那么在一次迭代中就可能同时找到多条增广路径了!

这里解释一下伪代码 :
1.初始情况:当前的匹配为空;
2.循环过程 3 和 4;
3.从中的未匹配的向量(或者端点)出发,通过BFS构建一条分层后的交替路;
4.通过DFS寻找交替路中最短的增广路集合,然后得到基于当前增广路的最大匹配解;
5.当找不到增广路后结束迭代;
6.返回最大匹配解。
- step1: 通过BFS来确立当前点的层次。请注意每次BFS迭代中我们都只去遍历那些未匹配的
,即
,如果一个点
属于层次
,就说明
在某条增广路径中最早出现的顺位是
。当遍历到当前层中出现
或者当前层为空集的时候结束这次BFS,并且按照结果得到交替路。
说明一下为什么遍历到当前层中出现时可以结束本次遍历,按照增广路径的定义,我们首位都需要是未匹配的点,在BFS是从一个
开始,在后续交替路中出现了
则说明我们找到了一条长度是偶数的交替路,进一步可以找到一条增广路径,因为我们每次都是找的最短的增广路径,所以一旦找到,我们就可以退出这次BFS遍历。
- step2:从BFS得到的交替路中去寻找增广路径,然后将增广路径中的端点按照当前匹配关系记录到matching列表中;
- step3:重复step1和step2,直到找不到增广路径,结束算法,返回最大匹配。
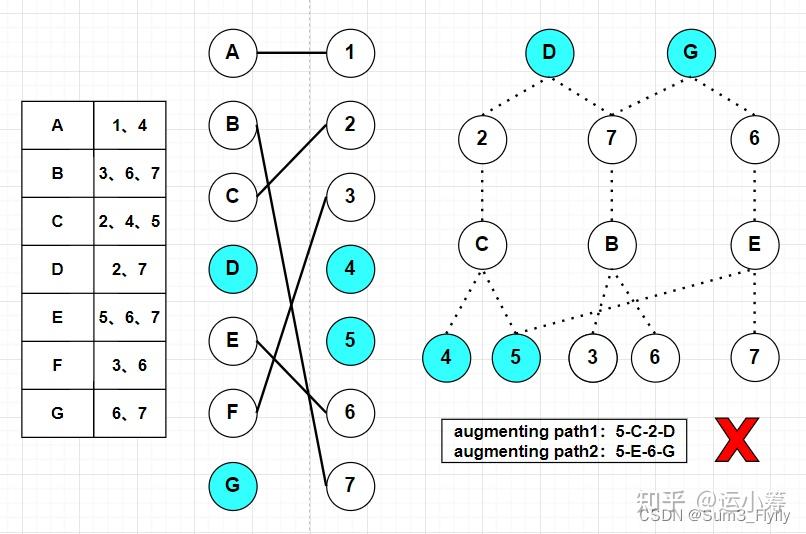
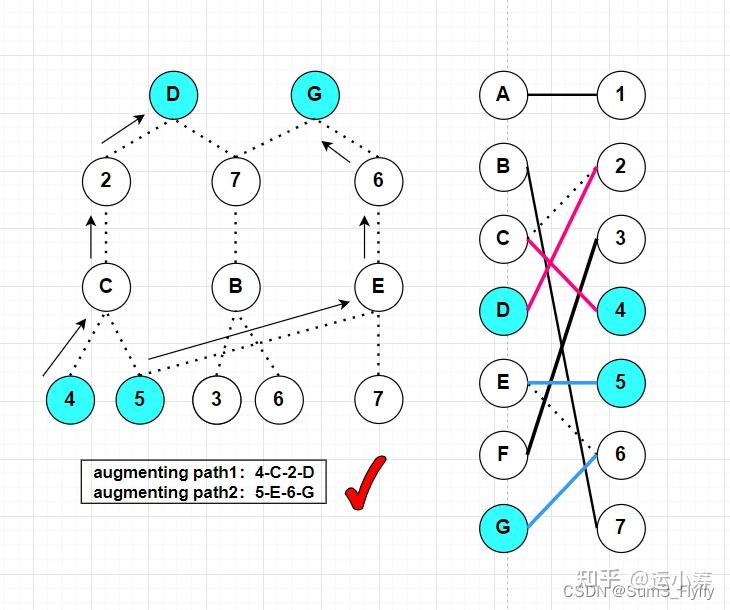
第一次找的增广路径是不可行的,因为点 同时出现在了两条增广路径中,在DFS找到当前增广路径后,然后将原本匹配的边断开,就得到当前的匹配关系,图中用了不同的颜色表示两条增广路径。
在计算复杂度之前我们先引用两个引理: 设有二部图 是最大配对数,
为当前匹配数。
- Lemma1:在
次迭代寻找增广路径后,增广路径的长度至少是
。
- Lemma2:
,其中
为当前迭代中最短的增广路径的长度。
设经过 次迭代,通过Lemma1有当前最短增广路径的长度为
;再由Lemma2得
,说明
这个增广路径的长度刚好可以覆盖这个匹配的差,也就是说经过 次迭代,我们就已经找到了所有的增广路径,所以有
。 又因为每次BFS和DFS迭代中最多遍历所有的边,所以有
。 所以HK算法的复杂度为
。
首先我们初始化和读取数据
# 二部图的匹配关系
graph = {'a': {1}, 'b': {1, 2}, 'c': {1, 2, 3}, 'd': {2, 3, 4}, 'e': {3, 4, 10}, 'f': {4, 5, 6}, 'g': {5, 6, 7},
'h': {7, 8}, 'i': {9}}
from copy import deepcopy
class HK_algorithm(object):
def __init__(self, graph):
"""
初始化和接受配对关系图,初步处理
:param graph:为了方便操作,二部图的左右集合我们用不同的数据类型来表示
"""
self._graph = deepcopy(graph)
self._left_set = set(self._graph.keys())
self._right_set = set()
self._matching = {}
self._dfs_paths = []
self._dfs_alternately = {}
self.iter_times = 0
# 处理 右端点 的端点,放入 self._right
graph_values = set
for value in self._graph.values():
for i in value:
self._right_set.add(i)
print(self._right_set)
# 为了找增广路径, 需要将右端点,可以连接的左端点处理成为一个相应的 graph 字典
for left_node in self._left_set:
for neighbour in self._graph[left_node]:
if neighbour not in self._graph:
# 防止重复
self._graph[neighbour] = set()
self._graph[neighbour].add(left_node)
else:
self._graph[neighbour].add(left_node)
然后我们定义一下BFS:
def breadth_first_search(self):
visited = set()
layers = [] # index=layer 按照层存储点 待遍历的点
layer = set()
for node in self._left_set:
if node not in self._matching:
layer.add(node)
layers.append(layer)
while True:
new_layer = set()
layer = layers[-1]
for node in layer:
if node in self._left_set:
visited.add(node)
for neighbour in self._graph[node]:
if neighbour not in visited and (
node not in self._matching or neighbour != self._matching[node]):
new_layer.add(neighbour)
else:
visited.add(node)
for neighbour in self._graph[node]:
if neighbour not in visited and (node in self._matching and neighbour == self._matching[node]):
new_layer.add(neighbour)
layers.append(new_layer)
if len(new_layer) == 0:
return layers
for node in new_layer:
if any(node in self._right_set and node not in self._matching for node in new_layer):
return layers
展示迭代过程部分结果
'''
after bfs:
layers=[{'i', 'e', 'a', 'g', 'c', 'd', 'f', 'h', 'b'},
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}]
layer_1=['i', 'e', 'a', 'g', 'c', 'd', 'f', 'h', 'b']
layer_2=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
'''
接下来定义一下DFS(一条路走到底):
def depth_first_search(self, free_node, node_in_layer_index, layers):
if node_in_layer_index == 0:
path = [free_node]
while self._dfs_alternately[free_node] != free_node:
path.append(self._dfs_alternately[free_node])
free_node = self._dfs_alternately[free_node]
self._dfs_paths.append(path)
return True
for neighbour in self._graph[free_node]:
if neighbour in layers[node_in_layer_index - 1]:
if neighbour in self._dfs_alternately:
continue
if (neighbour in self._left_set and (
free_node not in self._matching or neighbour != self._matching[free_node])) or (
neighbour in self._right_set and (
free_node in self._matching and neighbour == self._matching[free_node])):
self._dfs_alternately[neighbour] = free_node
if self.depth_first_search(neighbour, node_in_layer_index - 1, layers):
return True
return False
第一次DFS的迭代结果:
'''
after dfs:
?alternate_path={1: 1, 'b': 1, 2: 2, 'c': 2,
3: 3, 'e': 3, 4: 4, 'd': 4,
5: 5, 'g': 5, 6: 6, 'f': 6,
7: 7, 'h': 7, 8: 8,
9: 9, 'i': 9, 10: 10}
augmenting_path={1:'b', 2:'c', 3:'e', 4:'d',
5:'g', 6:'f',7:'h', 9:'i'}
'''
最后的max matching结果为:
'''
max matching:{'b': 2, 'c': 3, 'e': 10,
'd': 4, 'g': 5, 'f': 6,
'h': 7, 'i': 9, 'a': 1}
'''
讲解Hopcroft–Karp algorithm url: https://www.youtube.com/watch?v=lM5eIpF0xjA
维基百科-Hopcroft Karp algorithm
百度百科-霍普克洛夫特-卡普算法
百度百科-二分图 百度百科-宽度优先搜索
百度百科-深度优先搜索
匈牙利算法 https://zhuanlan.zhihu.com/p/208596378
欢迎关注我们的微信公众号 运小筹
运小筹公众号致力于分享运筹优化(LP、MIP、NLP、随机规划、鲁棒优化)、凸优化、强化学习等研究领域的内容以及涉及到的算法的代码实现。编程语言和工具包括Java、Python、Matlab、CPLEX、Gurobi、SCIP 等。欢迎广大同行投稿!欢迎大家关注我们的公众号“运小筹”以及粉丝群!
可以私信编辑 MunSum3(知乎id) 拉入读者群
【运小筹】于去年建立了【OR领域英文期刊论文写作帮帮群】,旨在分享OR领域期刊论文的好的表达,用法,以及写作经验和心得。
之前一直是内部交流,现开放加群。
对此有浓厚兴趣,强烈意愿,并承诺愿意分享,一起学习进步的小伙伴,想进群的,可以加
微信:Ssum3_Klaus
小编通过之后可以拉大家入群一起学习
强调:帮帮群旨在相互分享、相互提升写作能力,分享意愿不高的同学建议添加我们读者群讨论问题。
目前我们运小筹微信公众号已经有接近10000关注了,为了纪念这个里程碑,我们决定奖励
1. 第10000位粉丝
2. 截止2022年6月5日23:59分,【阅读最多】【分享最多】【赞赏最多】【留言最多】四个项目中排名前五的粉丝
将直接获得之前的全部月刊


预告:等到1w粉后,将会开放读者核心群,入群对象为较为活跃的粉丝群体,活跃指标从:公众号推文分享次数、群内分享互助次数等方面考察。在核心群的成员可以享受到一些额外的福利,例如:一些小编整理的资料(如Notice2的月刊以及下图,这只是冰山一角)等
友情提示:为了避免进入核心群就不再分享、讨论,核心群或定期重新洗牌

第89篇:优化算法 | Benders Decomposition: 一份让你满意的【入门-编程实战-深入理解】的学习笔记
第88篇:优化 | 史上最【皮】数学题求解的新尝试:一种求解器的视角 (Python调用Gurobi实现)
第87篇:优化 | 寻找新的建模视角——从直观解释对偶问题入手:以Cutting Stock Problem的对偶问题为例
第86篇:ORers‘ Bling Chat【03】 | 【高光聊天记录集锦】:运小筹读者群里那些热烈的讨论
第85篇:非线性优化 | 非线性问题线性化以及求解的详细案例及Python+Gurobi求解
第84篇:ORers' Bling Chat | 【高光聊天记录集锦-02】:运小筹读者群里那些热烈的讨论
第83篇:Machine-Learning–Based Column Selection for Column Generation
第82篇:最新!205页运小筹优化理论学习笔记发布(2021年9月--2022年3月)!
第81篇:【鲁棒优化】| 补充证明:为什么最优解一定满足取值等于绝对值(论文笔记:The Price of Robustness)
第80篇:【鲁棒优化】| 论文笔记:The Price of Robustness - 列不确定性模型部分的推导和一些思考
第79篇:ORers' Bling Chat | 【高光聊天记录集锦-01】:运小筹读者群里那些热烈的讨论
第78篇:优化| 手把手教你学会杉数求解器(COPT)的安装、配置与测试
第77篇:【教学视频】优化 | 线性化(2):连续变量 * 0-1变量的线性化
第76篇:【教学视频】优化 | 线性化:两个0-1变量相乘的线性化
第75篇:强化学习实战 | DQN和Double DQN保姆级教程:以Cart-Pole为例
第74篇:强化学习| 概念梳理:强化学习、马尔科夫决策过程与动态规划
第73篇:强化学习实战 | Q-learning求解最短路(SPP)问题
第72篇:鲁棒优化 | 以Coding入门鲁棒优化:以一个例子引入(二)
第71篇:鲁棒优化|基于ROME编程入门鲁棒优化:以一个例子引入(一)
第70篇:优化|含分式的非线性规划求解: 基于Outer Approximation的Branch-and-cut 算法及其Java实现
第69篇:科研工具 | 手把手教你玩转文献管理神器:Endnote
第68篇:相约深圳 | 2022 INFORMS 服务科学国际会议·征稿通知
第67篇:鲁棒优化| 利用rome求解鲁棒优化简单案例:以CVaR不确定性集为例
第65篇:最新!145页运小筹优化理论学习笔记发布(2021年4月--9月)!
第64篇:优化 | 手把手教你用Python调用SCIP求解最优化模型
第63篇:优化 | 随机规划案例:The value of the stochastic solution
第62篇:工具 | draw.io: 科研流程示意图必备大杀器
第61篇:优化 | 开源求解器SCIP的安装与入门教程(Windows+Python)
第60篇:优化|Gurobi处理非线性目标函数和约束的详细案例
第58篇:测试算例下载:《运筹优化常用模型、算法及案例实战:代码手册》
第57篇:鲁棒优化|分布式鲁棒优化转化为SOCP案例及代码实现(Python+RSOME)
第56篇:鲁棒优化 | 分布式鲁棒优化简单案例及实战(RSOME+Gurobi)
第55篇:【尾款+发货】|【代码手册】 《运筹优化常用模型、算法及案例实战:Python+Java
第52篇:【视频讲解】CPLEX的OPL语言:可视化的优化模型求解解决方案
第51篇:算法 | 基于英雄联盟寻路背景的A星算法及python实现
第50篇:【转发】清华大学深圳国际研究生院2021年物流工程与管理项目优秀大学生夏令营报名通知
第49篇:优化 | 精确算法之分支定界介绍和实现(附Python代码)
第47篇:【重新发布】|《运筹优化常用模型、算法及案例实战:Python+Java实现》 【代码手册】 开始预购啦!!!
第46篇:智慧交通可视化:手把手教你用Python做出行数据可视化-osmnx 包入门教程
第45篇:优化 | Pick and delivery problem的介绍与建模实现(二)
第43篇:元启发式算法 | 遗传算法(GA)解决TSP问题(Python实现)
第42篇:优化|视频详解Python调用Gurobi的应用案例:TSP
第38篇:浅谈 | P问题、NP问题、NPC问题、NP-Hard问题
第35篇:优化|高级建模方法(Gurobi):线性化表达小技巧
第34篇:深度强化学习介绍 | Deep Q Network——理论与代码实现
第32篇:优化 | Pick and delivery problem的简介与建模实现(一)
第30篇:“Learn to Improve”(L2I):ICLR文章分享 | 运用RL解决VRP问题
第29篇:线性规划求解小程序 | 基于Python 的Cplex 求解器图形化界面
第27篇:Julia安装与配置Jupyter Notebook
第26篇:期刊征文| IEEE TRANSACTIONS应对COVID-19的特刊征文消息速递
第25篇:两阶段随机规划(Two-stage Stochastic Programming):一个详细的例子
第23篇:Python调用Gurobi:Assignment Problem简单案例
第20篇:运筹学与管理科学TOP期刊揭秘 —Service Science
第19篇:手把手教你用Python实现Dijkstra算法(伪代码+Python实现)
第18篇:运筹学与管理科学大揭秘—TOP期刊主编及研究方向一览
第17篇:优化 | 手把手教你用Python实现动态规划Labeling算法求解SPPRC问题
第16篇:代码 | 运小筹GitHub项目上线啦,快来标星收藏吧!!
第14篇:优化| 手把手教你用Python实现Dijkstra算法(附Python代码和可视化)
第13篇:优化|手把手教你用Python调用Gurobi求解最短路问题
第11篇:优化| 手把手教你用Python调用Gurobi求解VRPTW
第10篇:优化 | 两阶段启发式算法求解带时间窗车辆路径问题(附Java代码)
第7篇:优化 | TSP中两种不同消除子环路的方法及Callback实现(Python调用Gurobi求解)
第6篇:元启发式算法 | 禁忌搜索(Tabu Search)解决TSP问题(Python代码实现)
第5篇:论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)
第4篇:优化|Shortest Path Problem及其对偶问题的一些探讨(附Python调用Gurobi实现)
第3篇:可视化|Python+OpenStreetMap的交通数据可视化(二):OpenStreetMap+Python画城市交通路网图
第1篇:Python+networkX+OpenStreetMap实现交通数据可视化(一):用OpenStreetMap下载地图数据
作者:张瑞三,四川大学,硕士在读 邮箱:zrssum3@stu.scu.edu.cn
审校:刘兴禄,清华大学,清华-伯克利深圳学院 邮箱:hsinglul@163.com





